7 hằng đẳng thức đáng nhớ lớp 7,8: Công thức và phát biểu bằng lời.

Bảy hằng đẳng thức đáng nhớ bao gồm các công thức toán học lớp 7 mà các em cần phải nhớ để áp dụng vào các bài tập sau này. Các bạn có thể tham khảo qua bài viết này để có cách áp dụng 7 hằng đẳng thức đáng nhớ vào giải bài tập dễ hiểu nhất nhé!

7 hằng đẳng thức đáng nhớ đầy đủ

a. Bình phương của một tổng

Phát biểu bằng lời: Bình phương của 1 tổng sẽ (bằng =) bình phương của số thứ nhất (cộng +) với 2 lần tích của số thứ nhất nhân với số thứ hai và (cộng +) với bình phương của số thứ hai.

Công thức:

Ví dụ:

(x + 2)² = x² + 2.x.2 + 2² = x² + 4x + 4
(x + 6)² – x² – 36 = (x² + 2.x.6 + 6²) – x² – 36 = 12x.

b. Bình phương của một hiệu

Phát biểu bằng lời: Bình phương của 1 hiệu sẽ (bằng =) bình phương của số thứ nhất (trừ –) đi 2 lần tích của số thứ nhất và số thứ hai sau đó (cộng +) bình phương với số thứ hai.

Công thức:

Ví dụ:

(x – 1)² = x² + 2.x.1 + 1² = x² – 2x + 1
(x – 5)² – x² – 25 = (x² + 2.x.5 + 5²) – x² – 25 = – 10x.

c. Hiệu 2 bình phương

Phát biểu bằng lời: Hiệu hai bình phương của hai số sẽ (bằng =) tổng hai số đó (nhân x) với hiệu hai số đó.

Công thức:

Ví dụ:

x² – 4 = (x – 2)(x + 2)
x² – 9 + 2(x + 3) = (x – 3)(x + 3) + 2(x + 3) = (x + 3)(x – 3 + 2) = (x + 3)(x – 1)

d. Lập phương của một tổng

Phát biểu bằng lời: Lập phương của 1 tổng hai số sẽ (bằng =) lập phương của số thứ nhất (cộng +) với 3 lần tích bình phương số thứ nhất nhân số thứ hai, (cộng +) với 3 lần tích số thứ nhất nhân với bình phương số thứ hai, (cộng +) với lập phương số thứ hai.

Công thức :

Ví dụ:

(x + 1)³ = x³ + 3.x².1 + 3.x.1² + 1³ = x³ + 3x² + 3x + 1
(x + 6)³ – 2x³ – 18.x² + 1 = (x³ + 3.x².6 + 3.x.6² + 6³) – 2x³ – 18.x² + 1 = – x³ + 108x + 217

e. Lập phương của một hiệu

Phát biểu bằng lời: Lập phương của 1 hiệu hai số sẽ (bằng =) lập phương của số thứ nhất (trừ –) đi 3 lần tích bình phương của số thứ nhất nhân với số thứ hai, (cộng +) với 3 lần tích số thứ nhất nhân với bình phương số thứ hai sau đó (trừ –) đi lập phương số thứ hai.

Công thức :

Ví dụ:

(x – 2)³ = x³ – 3.x².2 + 3.x.2² – 2³ = x³ – 6x² + 12x – 8
(x – 2)³ – x³ – 18.x² = (x³ + 3.x².2 + 3.x.2² + 2³) – x³ – 18.x² = – 12.x² + 12x + 8

g. Tổng 2 lập phương

Phát biểu bằng lời: Tổng của hai lập phương hai số sẽ (bằng =) tổng của hai số đó (nhân x) với bình phương thiếu của hiệu hai số đó.

Công thức:

Ví dụ:

x³ + 8 = x³ + 2³= (x + 2)(x² – 2x + 4)

h. Hiệu 2 lập phương

Phát biểu bằng lời: Hiệu của hai lập phương của hai số sẽ (bằng =) hiệu hai số đó (nhân x) với bình phương thiếu của tổng của hai số đó.

Công thức:

Ví dụ:

x³ – 8 = x³ – 2³= (x – 2)(x² + 2x + 4)

Bảy hằng đẳng thức mở rộng

a. Bộ hằng đẳng thức bậc 2

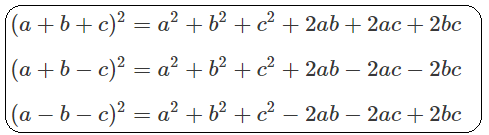
b. Bộ hằng đẳng thức bậc 3

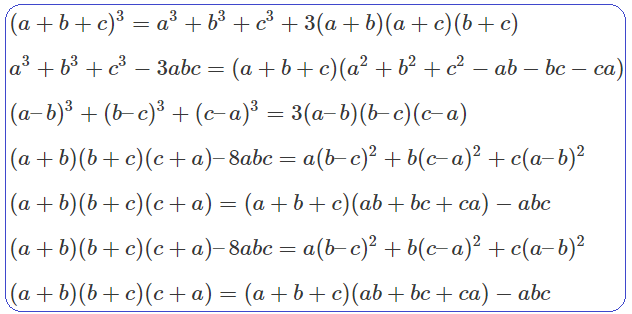
Xem thêm: S tam giác

Ứng dụng bảy hằng đẳng thức đáng nhớ vào các dạng bài tập

Bạn có thể sử dụng 7 hằng đẳng thức đáng nhớ vào các dạng bài tập như sau:

Tính giá trị của các biểu thức.
Chứng minh biểu thức A mà không phụ thuộc biến.
Áp dụng để tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức.
Chứng minh đẳng thức bằng nhau.
Chứng minh bất đẳng thức
Phân tích đa thức thành nhân tử.
Tìm giá trị của x
Thực hiện phép tính phân thức
Thực hiện phép tính phân thức

Tính giá trị của biểu thức

Bài 1 :tính giá trị của biểu thức : A = x² – 4x + 4 tại x = -1

Giải.

Ta có : A = x² – 4x + 4 = A = x² – 2.x.2 + 2² = (x – 2)²

Tại x = -1 : A = ((-1) – 2)²=(-3)²= 9

Vậy : A(-1) = 9

Chứng minh biểu thức A không phụ thuộc vào biến

B = (x – 1)² + (x + 1)(3 – x)

Giải.

B =(x – 1)² + (x + 1)(3 – x)

= x² – 2x + 1 – x² + 3x + 3 – x

= 4 : hằng số không phụ thuộc vào biến x.

Tìm giá trị nhỏ nhất của biểu thức

C = x² – 2x + 5

Giải.

Ta có : C = x² – 2x + 5 = (x² – 2x + 1) + 4 = (x – 1)²+ 4

Mà : (x – 1)²≥ 0 với mọi x.

Suy ra : (x – 1)²+ 4 ≥ 4 hay C ≥ 4

Dấu “=” xảy ra khi : x – 1 = 0 hay x = 1

Nên : C_min= 4 khi x = 1

Tìm giá trị lớn nhất của biểu thức

D = 4x – x²

Giải.

Ta có : D = 4x – x²= 4 – 4 + 4x – x²= 4 – (4 + x²– 4x) = 4 – (x – 2)²

Mà : -(x – 2)²≤ 0 với mọi x.

Suy ra : 4 – (x – 2)²≤ 4 hay D ≤ 4

Dấu “=” xảy ra khi : x – 2 = 0 hay x = 2

Nên : D_max= 4 khi x = 2.

Chứng minh đẳng thức

(a + b)³ – (a – b)³ = 2b(3a² + b²)

Giải.

VT = (a + b)³ – (a – b)³

= (a³ + 3a²b + 3ab² + b³) – (a³ – 3a²b + 3ab² – b³)

= a³ + 3a²b + 3ab² + b³ – a³ + 3a²b – 3ab² + b³

= 6a²b + 2b³

= 2b(3a² + b²) ->đpcm.

Vậy : (a + b)³ – (a – b)³ = 2b(3a² + b²)

Chứng minh bất đẳng thức

Biến đổi bất đẳng thức về dạng biểu thức A ≥ 0 hoặc A ≤ 0. Sau đó dùng các phép biến đổi đưa A về 1 trong 7 hằng đẳng thức.

Phân tích đa thức thành nhân tử

F = x² – 4x + 4 – y²

Giải.

Ta có : F = x² – 4x + 4 – y²

= (x² – 4x + 4) – y² [nhóm hạng tử]

= (x – 2)²– y² [đẳng thức số 2]

= (x – 2 – y )( x – 2 + y) [đẳng thức số 3]

Vậy : F = (x – 2 – y )( x – 2 + y)

Bài 1: A = x³ – 4x² + 4x

= x(x² – 4x + 4)

= x(x² – 2.2x + 2²)

= x(x – 2)²

Bài 2: B = x² – 2xy – x + 2y

= (x²– x) + (2y – 2xy)

= x(x – 1) – 2y(x – 1)

= (x – 1)(x – 2y)

Bài 3: C = x² – 5x + 6

= x² – 2x – 3x + 6

= x(x – 2) – 3(x – 2)

= (x – 2)(x – 3)

Tìm x. biết :

x² ( x – 3 ) – 4x + 12 = 0

Giải.

x² ( x – 3 ) – 4x + 12 = 0

x² ( x – 3 ) – 4(x – 3 ) = 0

( x – 3 ) (x² – 4) = 0

( x – 3 ) (x – 2)(x + 2) = 0

( x – 3 ) = 0 hay (x – 2) = 0 hay (x + 2) = 0

x = 3 hay x = 2 hay x = –2

vậy : x = 3; x = 2; x = –2

Thực hiện phép tính phân thức

Tính giá trị của phân thức M = $\frac{x^3-1}{x^2 -2x+1}$ tại x = –1

Giải.

ta có : M = $\frac{(x-1)(x^2+x+1)}{(x -1)^2}$

= $\frac{x^2+x+1}{x -1}$

Khi x = -1 : M = $\frac{(-1)^2+(-1)+1}{-1 -1} =\frac{-1}{2}$

Vậy : M = $=\frac{-1}{2}$ tại x = -1 .

Trên đây là toàn bộ 7 hằng đẳng thức đáng nhớ mà các em cần ghi nhớ công thức và lắm được các dạng bài tập về bẩy hằng đẳng thức đáng nhớ để áp dụng vào làm bài tập hiệu quả.

Bảng Các Công Thức Lượng Giác Sin Cos Lớp 10, 11 Cơ Bản, Nâng Cao